Axiomatic Attribution for Deep Networks(Mukund Sundararajan et al.)에서 나온 개념이다.
일반적으로 우리가 사용하는 딥러닝 모델은 설명이 힘든 블랙박스 모델이다. 대부분의 딥러닝 모델은 온갖 비선형성을 고려하고, 변수들을 조합하고, 수많은 파라미터(weight etc)를 가진다. 따라서 이러한 모델의 매커니즘을 인간이 알아들을 수 있도록 설명하는 것은 굉장히 어렵다.(이러한 task를 attribution task라고 한다)
하지만 어렵다고 그냥 내버려 둬서는 안된다. 우리의 모델이 accuracy가 높더라도 잘못된 정보를 바탕으로 예측 또는 분류를 진행하고 있을 수도 있기 때문이다. 예를 들어 우리에게 강아지 이미지와 동물 이미지를 잘 분류하는 모델이 있다고 가정해보자. 만약, 우리의 모델이 강아지 이미지를 강아지라고 분류하지만 강아지가 아닌 강아지의 목줄을 바탕으로 이러한 결론을 내린다면, 이 모델은 앞으로 문제를 발생시킬 확률이 높으며 모델 수정이 수반되어야 한다. 따라서 우리는 딥러닝 모델도 이해하기 위해 노력해야한다.

Integrated Gradients(IG)모델은 다양한 딥러닝 모델들을 설명하기 위한 모델이다. 이미지처리, 자연어처리, 정형 데이터 등 다양한 분야에 적용가능하고 대규모 네트워크에도 적용이 가능하기 때문에 특히 인기가 있다.
우선 IG의 intuition에 대해 간단히 설명해보겠다. 우리가 어떠한 모델의 학습을 마치고 이를 이용할 때, 우리가 가지게되는 변수는 더 이상 weight가 아닌 input data가 된다. 학습이 끝난 우리의 모델이 반환하는 prediction값은 input data, 즉 feature value로 이루어진 벡터에 의해 정해지는 것이다. 그리고 이 feature value가 결과에 미치는 영향력은 feature value * gradient로 구할 수 있다.

*first-order Tayer polynomial :

아래는 IG를 구하는 방법이다. 논문에서 가장 중요한 부분이다.




interpolation을 통해 baseline의 feature value와 input data의 feature value 사이 값들을 여러 개 생성할때 baseline은 informationless input이어야 한다. ex) 검은색 이미지, 빈 텍스트, 0으로 임베딩된 벡터
검은색 이미지를 서서히 밝게 하면서 누적되는 gradients를 평균하는 것이다(path method). 왜 그래야할까?
1) Accumulate pixel x's local gradients and attribute its importance as a score for how much it adds or subtracts to your model's overall output class probability. 또한, Interpolation path에 따른 모델의 예측값 변화를 볼 수도 있다.
2) Sensitivity, Implementation Invariance 만족을 위해서이다. 이 논문에서는 attribution methods가 꼭 만족해야하는 요소로 Sensitivity와 Implementation Invariance를 이야기한다. 이 두가지는 attribution task을 수행할 시 반드시 만족시켜야 하는 axiom(공리 : 가장 기초적인 근거가 되는 명제)이다.
(1) Axiom : Sensitivity
모든 input 과 baseline 사이에서 하나의 특정 feature의 value 차이가 prediction값의 차이를 불러오면, 그 feature의 영향력은 0이 아니어야 한다. sensitivity가 없거나 부족하면 gradients가 irreleveant features에 집중하게 된다.
EX) 간단하게 f(x) = 1 - ReLU(1-x) 를 생각해보자. x가 0 일 경우 f(0)는 0이다. 하지만 x가 2일 경우 f(2)는 1이다. sensitivity axiom에 따르면 이는 서로 다른 prediction 값을 불러오기 때문에 gradients는 서로 달라야 한다. 하지만 여기서 gradient는 동일하게 0이다. 이러한 경우를 회피하고 sensitivity를 만족시키기 위해서 여러장의 interpolated images에 대해 gradients를 구하고 이를 적분하는 것이다.
(2) Axiom : Implementation Invariance
만약 모든 inputs에 대해 서로 다른 모델들이 동일한 outputs를 내뱉는다면, 이 모델들은 기능적으로 동등하며 각 입력이 기여하는 정도 또한 두 모델에서 같아야한다.
(+) Axiom : Completeness
input과 baseline의 값들을 function에 넣어 얻은 output들의 차이는 feature들의 attribution과 대등해야 한다.
이 논문에서 IG는 Completeness라는 추가적 Axiom을 만족한다고 한다.
우리는 이 Axiom들을 만족하는 IG를 이용해 어떠한 픽셀들이 이미지의 분류에 지대한 영향을 미쳤는지 알 수 있다. 우선 우리는 이 모델이 비선형적이라는 것을 명심해야한다. input을 interpolate하여 여러 input을 생성하고 이들의 gradient를 적분함으로써 우리는 특정 픽셀의 영향력을 어느정도 일반화시켜 이해할 수 있다.
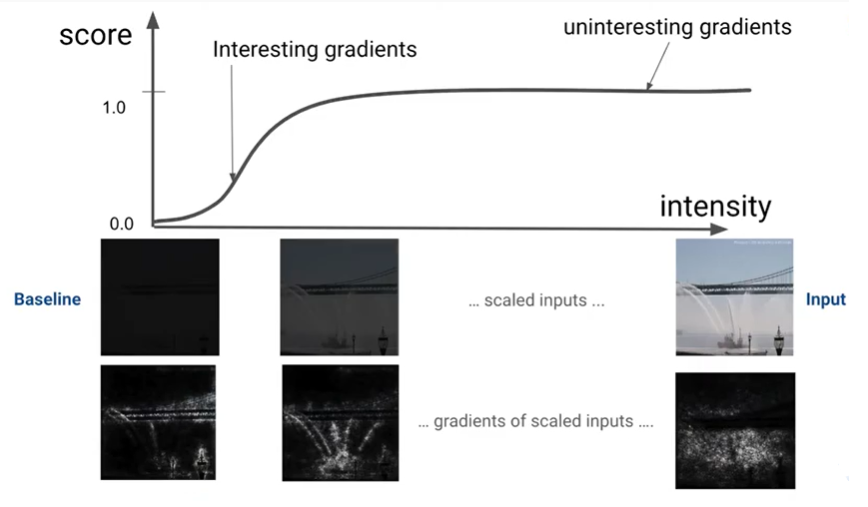
생성된 이미지들의 각 픽셀마다의 gradient가 나타날 것이고 이 gradient들을 적분하면 전반적인 픽셀의 아웃풋에 대한 영향력이 나타난다.
Reference :
Mukund Sundararajan et al., Axiomatic Attribution for Deep Networks, ICML 2017
Fiddler Labs의 Ankur Taly 박사님의 Youtube - AI Explained: What are Integrated Gradients? www.youtube.com/watch?v=9AaDc35JYiI
'deeplearning' 카테고리의 다른 글
| Transformer, BERT와 관련해서 읽어보면 좋은 블로그 모음 (0) | 2020.10.16 |
|---|---|
| CRF를 이용한 Named Entity Recognition (0) | 2020.09.18 |
| Optimization - Momentum, RMSProp, Adam (0) | 2020.08.21 |
| Graph Convolutional Neural Networks (GCN) (0) | 2020.08.11 |
| Gensim Word2Vec Fine-tuning (1) | 2020.06.22 |



